通过Single/Double Rotation来确保AVL Tree的成立|学习记录
AVL树拥有O(logN)的查找和删除速度,这也是我们创建这种数据结构的原因,但是,一次删除或者添加操作就可能破坏其脆弱的结构,因此我们需要Single/Double Rotation来保证其结构的正确。
什么是AVL树
AVL tree is binary search tree with self balancing ability.
Its height difference between the right and left subtree of all nodes not greater than one.
简单来说,就是一个每个叶子的高度差不大于一的二叉搜索树。
S/D Rotation
为什么需要
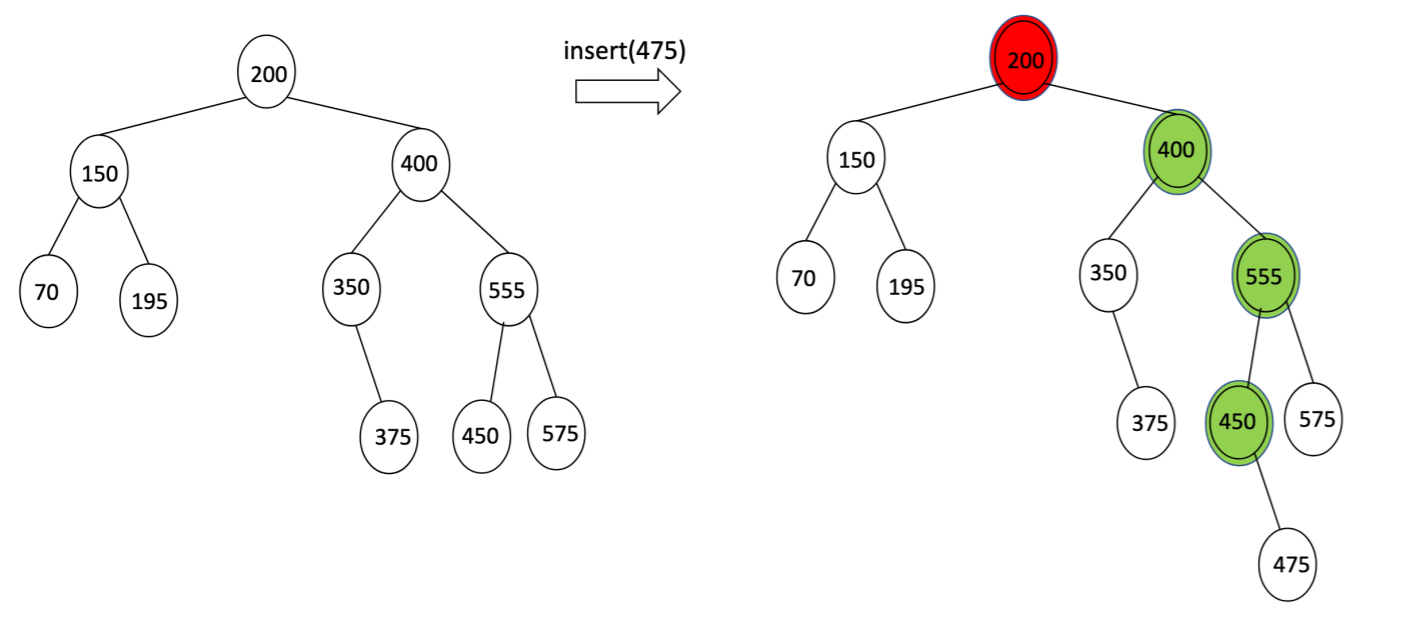
如图所示,一次简单的插入操作后,200右边的高度变成了4,而左边为2,叶子的高度差大于1,直接破坏了AVL树的结构。通过Single/Double Rotation,我们可以恢复其结构。
使用时机与选择
这边有一个平衡系数用来判断其高度差。
即 左子树的高度 - 右子树的高度 = 该节点的平衡系数
简单来说,就是找,找到某个节点,其左右子树高度差大于二,那么此时就需要旋转了。一般来说,会有这么四种情况:
- 左边子树的左节点过长(Left – Left Rotation)
- 右边子树的右节点过长(Right – Right Rotation)
- 右边子树的左节点过长(Right – Left Rotation)
- 左边子树的右节点过长(Left – Right Rotation)
前两种情况使用Single Rotation即可解决,后两种情况较为复杂,需要使用Double Rotation来解决。
Single Rotation
上图就是一个R-R Rotation,即右子树的右节点过长。正常来说,我们需要按照以下步骤:
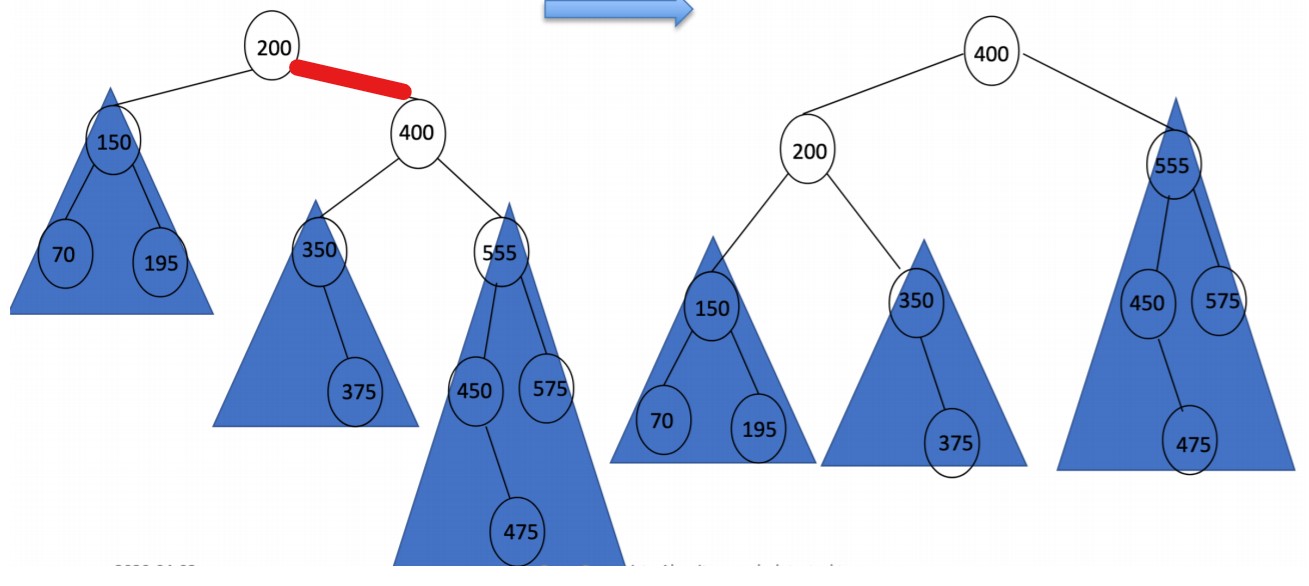
- 找到不平衡的点,即其平衡系数绝对值大于1(注意,这个点可能有好多个,应该选择层数最高的那个)
- 如图标红的线就是我们要移动的,我们将200绕着400逆时针旋转,把350挤掉(350与400的连线断开),使200成为400的左节点
- 将350作为200的右节点连接起来
- 完成
一个印象可能不够深刻,下图可以当一个练习。
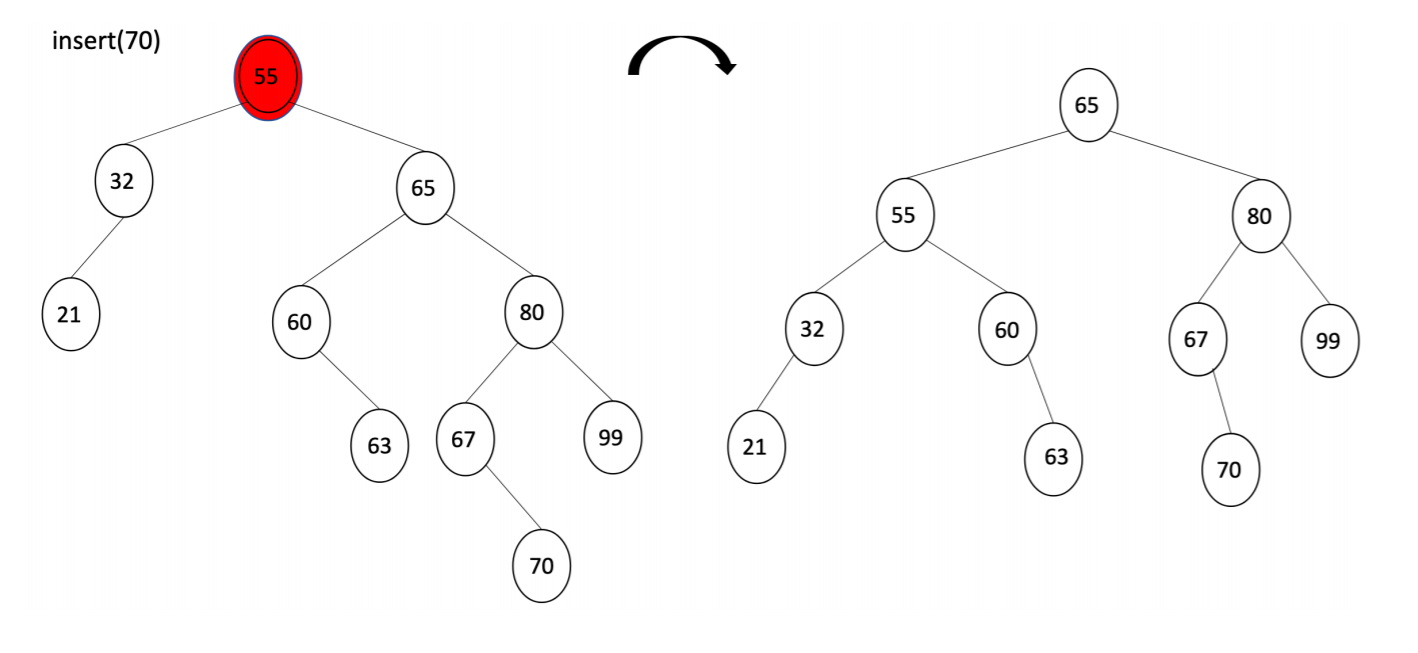
Double Rotation
我们可以简单粗暴的理解成两次Single Rotation,以下是我们的操作流程:
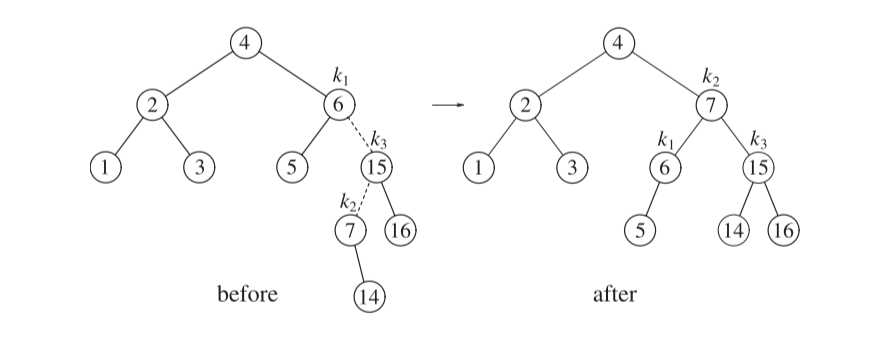
-
同样的,找到不平衡的点,这里4,6都是,我们应该选择6
-
两条虚线就是我们要移动的线,我们首先移动下面一条(即7和15连着的线),我们将15绕着7顺时针旋转,挤掉14,再将14拼接在15上,结果如图所示(仅展示移动部分)
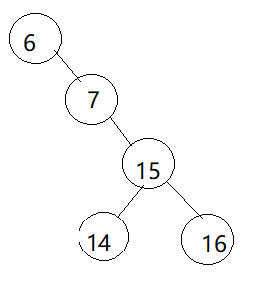
-
同样的操作,移动6和15连着的线,将6绕着7逆时针旋转(这时候没有需要挤掉的数),将其变为7的左节点,结束
小结
这块内容上课时没听清楚,花了挺久的时间才整明白,感觉网上的资料写的不是特别详细,只有开始与结果图,没有过程讲解,所以我就来写一写,既强化下记忆,也能帮助有需要的人~