Jun 2, 2022

Bag, Stack and Queue的构造与运用|Algorithms, Part1|第二周

引言

记录一下刷Coursera上《Algorithms, Part1》课程的所学内容。主要包括复现一些课上经典的数据结构与算法（C++），以及每周课程作业的部分（Java）。如有错误之处，欢迎纠正。

对应的Github链接：IronHao/MyAlgorithmBook (github.com)

正文

本周内容比较多，分两篇来总结。这是第一部分，主要包含Bag, Stack and Queue的内容。

课程内容

Bag, Stack and Queue是最基础的三个数据结构，我们后续更复杂的算法和数据结构都基于这几个数据结构。

在具体学习了解各个数据结构之前，书本上给我们指明了数据结构的三个最优设计目标：

它可以处理任意类型的数据；
所需的空间总是和集合的大小成正比；
操作所需的时间总是和集合的大小无关。

这次在代码实现上，我使用模板类（template）来实现泛型的效果[为了实现目标1]。同时为了代码的整洁，我将头文件（.h）与源文件（.cpp）分离。

这中间还遇到了一些小问题，具体可以查看这边。

另外因为我使用偷懒的办法（再导入.cpp文件）去解决这个问题，为了防止重复编译，要在每个文件开头写上#pragma once保证只执行一次编译。

另外，为了简化内容，我并没有对一些极端情况进行异常处理，如栈为空时尝试从栈顶弹出元素，正常应该抛出一个栈为空的异常报错，然而我选择默认弹出一个T()的返回值。

接下来让我们逐个看一看。

Node

因为在这里我会分别使用**链式存储（链表）和顺序存储（数组）*两种方法去实现这几个数据结构（Bag仅用链表，因为数组实现感觉也没什么特别的）*。所以我们需要先实现一下链表中的这个结点类Node。

顺带总结下链表和数组各自的优劣：（来自书本）

数据结构优点缺点

数组通过索引可以直接访问任意元素在初始化时就需要知道元素的数量

链表使用的空间大小和元素数量成正比需要通过引用访问任意元素（存引用需要增加内存开销）

数据结构	优点	缺点
数组	通过索引可以直接访问任意元素	在初始化时就需要知道元素的数量
链表	使用的空间大小和元素数量成正比	需要通过引用访问任意元素（存引用需要增加内存开销）

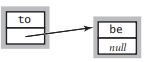
这个数据结构应该包含两个基本的变量：

T _val：一个T类型的值。
Node<T>* _next：一个指向下一个结点的指针，没有则设为nullptr（空）。

大致如图所示：

实现代码如下：

/* Node.h */

#pragma once

using namespace std;

/* The one node in Linked-list */
template <class T>
class Node
{
private:
    T _val;
    Node<T>* _next;
public:
    Node(T val);
    Node(T val, Node<T>* next);
    ~Node();

    /* Get methods */
    T getVal();
    Node* getNext();
    
    /* Set methods */
    void setVal(T val);
    void setNext(Node<T>* next);
};

/* Node.cpp */

#pragma once

#include "Node.h"

template <class T>
Node<T>::Node(T val)
{
    setVal(val);
    setNext(nullptr);
}

template <class T>
Node<T>::Node(T val, Node<T>* next)
{
    setVal(val);
    setNext(next);
}

template <class T>
Node<T>::~Node() {};

/* Get methods */
template <class T>
T Node<T>::getVal() { return _val; }

template <class T>
Node<T>* Node<T>::getNext() { return _next; }

/* Set methods */
template <class T>
void Node<T>::setVal(T val) { _val = val; }
    
template <class T>
void Node<T>::setNext(Node<T>* next) { _next = next; }

Bag

背包（Bag）是一种不支持从中删除元素的集合数据类型，同时，背包里的元素也不存在确定的拿取（访问）顺序。

它的目的就是帮助用例收集元素并迭代遍历所有收集到的元素，且这些元素的处理顺序应该是不重要的。

这个数据结构应该包含以下的几个基本方法：

void add(T val)：将一个元素添加到包中。
bool isEmpty()：判断包是否为空。
int size()：返回背包中的元素数量。
T* elements()：返回一个装有背包中所有元素的数组。

因为背包并没有明确它的访问顺序，在add()中的添加位置也可以任意。考虑到我这边是使用链表来实现，所以我会在链表头部插入新节点，这样每次添加的时间复杂度为常数$O(1)$，减少开销。elements()的话，我选择按照链表的顺序从头逐个读取并存入数组。

实现代码如下：

/* Bag.h */

#pragma once

#include "Node.h"
#include "Node.cpp"

using namespace std;

/* 
 * Bag data structure, no specific store way, here we use linked-list to store the data.
 * It has only add() method, no remove() method.
 * The element in bag has no specific order.
 */
template <class T>
class Bag
{
private:
    Node<T>* _head;
    int _size;
public:
    Bag();
    ~Bag();

    /* Insert in the head, no need to traverse, time complexity: O(1) */ 
    void add(T val);

    /* Return whether the bag is empty or not */
    bool isEmpty();

    /* Return the number of elements in bag */
    int size();

    /* Store the value in array and return */
    T* elements();
};

/* Bag.cpp */

#pragma once

#include "Bag.h"

template<class T>
Bag<T>::Bag() 
{
    _head = nullptr;
    _size = 0;    
}

template<class T>
Bag<T>::~Bag() {}

/* Insert in the head, no need to traverse, time complexity: O(1) */ 
template<class T>
void Bag<T>::add(T val)
{
    Node<T>* n = new Node<T>(val);
    n->setNext(_head);
    _head = n;
    _size++;
}

/* Return whether the bag is empty or not */
template<class T>
bool Bag<T>::isEmpty() { return _size == 0; }

/* Return the number of elements in bag */
template<class T>
int Bag<T>::size() { return _size; }

/* Store the value in array and return */
template<class T>
T* Bag<T>::elements()
{
    T* ans = new T[_size];
    int count = 0;
    Node<T>* cur = _head;
    while (cur != nullptr)
    {
        ans[count] = cur->getVal(); 
        cur = cur->getNext();
        count++;
    }
    return ans;
};

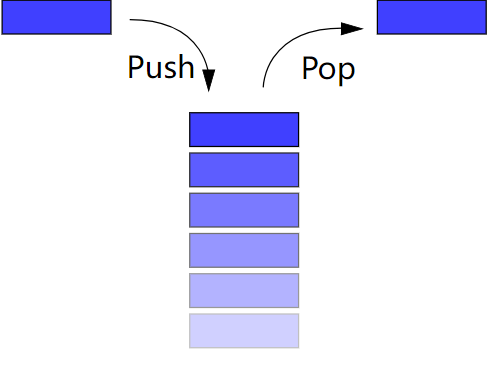
Stack

栈（Stack），或者叫做下压栈，是一种基于后进先出（LIFO, Last In Frist Out）策略的集合类型。

生活中电子邮箱的默认排序（最新的在最上面），以及浏览器的回退按钮等，都基于栈这种后进先出的策略实现。

它默认最新的（刚放到栈顶的）拥有最高的优先级。

这个数据结构应该包含以下的几个基本方法：

void push(T item)：将一个元素添加到栈顶。
T pop()：弹出（返回并删除）栈顶的元素。
T top()：返回栈顶的元素，不删除。
bool isEmpty()：查看栈是否为空，为空返回true，否则返回false。
int count()：返回栈内的元素个数。

栈这边的话既可以使用链式存储，也可以使用顺序存储。对于这两种，分别有一些细节需要考虑：

对于链式存储，我们只需要维护一个指向栈顶元素的指针和元素总数的Int型变量即可。元素总数没啥好说，push+1，pop-1即可。栈顶指针的话，我们将其认为为链表头部，每次我们都在头部添加一个新的，删除则是将指针指向下一个然后删除原先的头指针即可。
对于顺序存储，我们只需要维护元素总数的Int型变量即可，数组内非空的最后一个元素就是我们的栈顶。关键就在于数组大小的动态更改，因为数组本身大小在分配内存时就限定死了，要想改变大小，只能重新分配一个新的数组，并将原先的值逐个复制过去，这是一个比较大的开销，因为需要遍历整个数组（时间复杂度$O(n)$）。我们这里采取的策略是：
- 当数组满了，我们将数组容量翻倍（即$*2$)，并将原来的数据转移到新数组中；
- 当数组内元素数量减到数组容量的$\frac{1}{4}$时，我们将数组容量减半（即$\frac{1}{2}$）。
这是一种比较高效的做法，具体证明就不展开了。

实现代码如下：（ArrayStack表示使用顺序存储，LinkedListStack表示使用链式存储）

/* ArrayStack.h */

#pragma once

/* 
 * Stack data structure, array implementation. FILO.
 */
template <class T>
class ArrayStack
{
private:
    T* _arr;
    int _size;
    int _count;

    /* Return whether the stack is full or not */
    bool isFull();
    /* Resize the stack to the 'newSize' */
    void resize(int newSize);

public:
    ArrayStack();
    ~ArrayStack();

    /* Push the 'item' to the top of the stack */
    void push(T item);
    /* Pop(delete) and return the item in the top of the stack */
    T pop();
    /* Get the item in the top of the stack, no delete */
    T top();
    /* Return whether the stack is empty or not */
    bool isEmpty();
    /* Return the size (allocate memory) of the stack */
    int size();
    /* Return the number of items in the stack */
    int count();
};

/* ArrayStack.cpp */

#pragma once

#include "ArrayStack.h"

template<class T>
ArrayStack<T>::ArrayStack()
{
    _size = 1;
    _count = 0;
    _arr = new T[_size];
}

template<class T>
ArrayStack<T>::~ArrayStack()
{
    delete[] _arr;
}

/* Return whether the stack is full or not */
template<class T>
bool ArrayStack<T>::isFull() { return _size == _count; }

/* Resize the stack to the 'newSize' */
template<class T>
void ArrayStack<T>::resize(int newSize)
{
    T* tempArr = new T[newSize];
    for (int i = 0; i < count(); i++)
        tempArr[i] = _arr[i];
    delete[] _arr;
    _arr = tempArr;
    _size = newSize;
}

/* Push the 'item' to the top of the stack */
template<class T>
void ArrayStack<T>::push(T item)
{
    // Resize the array(Double the size of array) if the stack is full
    if (isFull())
        resize(size()*2);
    // Push the item
    _arr[_count++] = item;
}

/* Pop(delete) and return the item in the top of the stack. Return nullptr if the stack is empty */
template<class T>
T ArrayStack<T>::pop()
{
    // Pop the item
    T ans = T();
    if (!isEmpty())
        ans = _arr[--_count];
    // Resize the array(halve the size) if the count is one-quarter full
    if (count() > 0 && count() == size() / 4)
        resize(size()/2);
    return ans;
}

/* Get the item in the top of the stack, no delete. Return nullptr if the stack is empty */
template<class T>
T ArrayStack<T>::top() 
{
    T ans = T();
    if (!isEmpty())
        ans = _arr[_count-1]; 
    return ans; 
}

/* Return whether the stack is empty or not */
template<class T>
bool ArrayStack<T>::isEmpty() { return _count == 0; }

/* Return the size (allocate memory) of the stack */
template<class T>
int ArrayStack<T>::size() { return _size; }

/* Return the number of items in the stack */
template<class T>
int ArrayStack<T>::count() { return _count; }

/* LinkedListStack.h */

#pragma once

#include "Node.h"
#include "Node.cpp"


/* 
 * Stack data structure, linked-list implementation. FILO.
 */
template<class T>
class LinkedListStack
{
private:
    /* data */
    Node<T>* _top;
    int _count;
public:
    LinkedListStack();
    ~LinkedListStack();

    /* Push the 'item' to the top of the stack */
    void push(T item);
    /* Pop(delete) and return the item in the top of the stack */
    T pop();
    /* Get the item in the top of the stack, no delete */
    T top();
    /* Return whether the stack is empty or not */
    bool isEmpty();
    /* Return the number of items in the stack */
    int count();
};

/* LinkedListStack.cpp */

#pragma once

#include "LinkedListStack.h"

template<class T>
LinkedListStack<T>::LinkedListStack()
{
    _top = nullptr;
    _count = 0;
}

template<class T>
LinkedListStack<T>::~LinkedListStack()
{
    delete _top;
}

/* Push the 'item' to the top of the stack */
template<class T>
void LinkedListStack<T>::push(T item)
{
    Node<T>* temp = new Node<T>(item);
    temp->setNext(_top);
    _top = temp;
    _count++;
}

/* Pop(delete) and return the item in the top of the stack */
template<class T>
T LinkedListStack<T>::pop()
{
    T ans;
    if (!isEmpty())
    {
        ans = _top->getVal();
        Node<T>* temp = _top;
        _top = _top->getNext();
        delete temp;
        _count--;
    }
    else
        ans = T();
    return ans;
}

/* Get the item in the top of the stack, no delete */
template<class T>
T LinkedListStack<T>::top()
{
    T ans;
    if (!isEmpty())
        ans = _top->getVal();
    else
        ans = T();
    return ans;
}

/* Return whether the stack is empty or not */
template<class T>
bool LinkedListStack<T>::isEmpty() { return _count == 0; }

/* Return the number of items in the stack */
template<class T>
int LinkedListStack<T>::count() { return _count; }

Queue

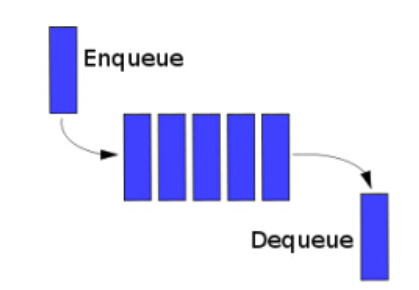
队列（Queue），或者叫做先进先出队列，是一种基于先进先出（FIFO, First In First Out）策略的集合类型。

它就像我们生活中排队一样，遵从先来后到的原则，认为最早来的拥有最高的优先级。

通过使用队列，我们可以在保存元素的同时保存它们的相对顺序，即让它们的入列顺序与出列顺序保持一致（栈则刚好相反，为逆序）。

这个数据结构应该包含以下的几个基本方法：

void enqueue(T item)：将一个元素添加到队尾。
T dequeue()：弹出（返回并删除）队头的元素。
T first()：返回队头的元素，不删除。
T last()：返回队尾的元素，不删除。
bool isEmpty()：查看队列是否为空，为空返回true，否则返回false。
int count()：返回队列内的元素个数。

同样，队列这边的话也既可以使用链式存储，也可以使用顺序存储。对于这两种，分别有一些细节需要考虑：

对于链式存储，我们只需要维护两个指针（一个指向队头的元素，一个指向队尾的元素）和元素总数的Int型变量即可。元素总数没啥好说，enqueue+1，dequeue-1即可。指针的话就是简单的在删除和添加操作时更新头和尾指针即可。正常情况下，enqueue只用更新队尾指针，dequeue只用更新队头指针。但要注意为空的边界条件（从一个元素变为零个/从零个变为一个），此时两个指针都需要维护。
对于顺序存储，我们有两种选择：
- 维护一个指向队头的下标+元素总数的Int型变量，队尾由队头+元素总数-1得出。
- 维护一个指向队头的下标+一个指向队尾的下标，元素总数由队尾-队头+1得出。
在这里我选择第一种。另外，为了充分利用空间，我们将数组理解为一个环（即对于大小为$n$的数组$arr$，最后一个数组元素$arr[n-1]$的下一个元素为$arr[0]$)。所以我们这里要用到取余%来实现，具体见代码。

实现代码如下：（ArrayQueue表示使用顺序存储，LinkedListQueue表示使用链式存储）

/* ArrayQueue.h */

#pragma once

/* 
 * Queue data structure, linked-list implementation. FIFO.
 */
template<class T>
class ArrayQueue
{
private:
    T* _arr;
    int _head;
    int _size;
    int _count;

    /* Return whether the queue is full or not */
    bool isFull();
    /* Resize the queue to the 'newSize' */
    void resize(int newSize);
public:
    ArrayQueue();
    ~ArrayQueue();

    /* Insert a new item onto queue(tail of the queue) */
    void enqueue(T item);
    /* Remove and return the item least recently added(head of the queue) */
    T dequeue();
    /* Return the item least recently added without removing */
    T first();
    /* Return the item latest recently added without removing */
    T last();
    /* Return whether the queue is empty or not */
    bool isEmpty();
    /* Return the size (allocate memory) of the queue */
    int size();
    /* Return the number of items in queue */
    int count();
};

/* ArrayStack.cpp */

#pragma once

#include "ArrayStack.h"

template<class T>
ArrayStack<T>::ArrayStack()
{
    _size = 1;
    _count = 0;
    _arr = new T[_size];
}

template<class T>
ArrayStack<T>::~ArrayStack()
{
    delete[] _arr;
}

/* Return whether the stack is full or not */
template<class T>
bool ArrayStack<T>::isFull() { return _size == _count; }

/* Resize the stack to the 'newSize' */
template<class T>
void ArrayStack<T>::resize(int newSize)
{
    T* tempArr = new T[newSize];
    for (int i = 0; i < count(); i++)
        tempArr[i] = _arr[i];
    delete[] _arr;
    _arr = tempArr;
    _size = newSize;
}

/* Push the 'item' to the top of the stack */
template<class T>
void ArrayStack<T>::push(T item)
{
    // Resize the array(Double the size of array) if the stack is full
    if (isFull())
        resize(size()*2);
    // Push the item
    _arr[_count++] = item;
}

/* Pop(delete) and return the item in the top of the stack. Return nullptr if the stack is empty */
template<class T>
T ArrayStack<T>::pop()
{
    // Pop the item
    T ans = T();
    if (!isEmpty())
        ans = _arr[--_count];
    // Resize the array(halve the size) if the count is one-quarter full
    if (count() > 0 && count() == size() / 4)
        resize(size()/2);
    return ans;
}

/* Get the item in the top of the stack, no delete. Return nullptr if the stack is empty */
template<class T>
T ArrayStack<T>::top() 
{
    T ans = T();
    if (!isEmpty())
        ans = _arr[_count-1]; 
    return ans; 
}

/* Return whether the stack is empty or not */
template<class T>
bool ArrayStack<T>::isEmpty() { return _count == 0; }

/* Return the size (allocate memory) of the stack */
template<class T>
int ArrayStack<T>::size() { return _size; }

/* Return the number of items in the stack */
template<class T>
int ArrayStack<T>::count() { return _count; }

/* LinkedListQueue.h */

#pragma once

#include "Node.h"
#include "Node.cpp"

/* 
 * Queue data structure, linked-list implementation. FIFO.
 */
template<class T>
class LinkedListQueue
{
private:
    Node<T>* _first;
    Node<T>* _last;
    int _count;
public:
    LinkedListQueue();
    ~LinkedListQueue();

    /* Insert a new item onto queue(tail of the queue) */
    void enqueue(T item);
    /* Remove and return the item least recently added(head of the queue) */
    T dequeue();
    /* Return the item least recently added without removing */
    T first();
    /* Return the item latest recently added without removing */
    T last();
    /* Return whether the queue is empty or not */
    bool isEmpty();
    /* Return the number of items in queue */
    int count();
};

/* LinkedListQueue.cpp */

#pragma once

#include "LinkedListQueue.h"

template<class T>
LinkedListQueue<T>::LinkedListQueue()
{
    _first = nullptr;
    _last = nullptr;
}

template<class T>
LinkedListQueue<T>::~LinkedListQueue()
{
    delete _first;
    delete _last;
}
    
/* Insert a new item onto queue(tail of the queue) */
template<class T>
void LinkedListQueue<T>::enqueue(T item)
{
    Node<T>* temp = new Node<T>(item);
    if (!isEmpty())
    {
        _last->setNext(temp);
        _last = temp;
    }
    else
    {
        _last = temp;
        if (_first == nullptr)
            _first = temp;
    }
    _count++;
}
    
/* Remove and return the item least recently added(head of the queue) */
template<class T>
T LinkedListQueue<T>::dequeue()
{
    T ans;
    if (!isEmpty())
    {
        ans = _first->getVal();
        Node<T>* temp = _first;
        _first = _first->getNext();
        delete temp;
        _count--;
    }
    else
        ans = T();
    return ans;
}

/* Return the item least recently added without removing */
template<class T>
T LinkedListQueue<T>::first()
{
    T ans;
    if (!isEmpty())
        ans = _first->getVal();
    else
        ans = T();
    return ans;
}
/* Return the item latest recently added without removing */
template<class T>    
T LinkedListQueue<T>::last()
{
    T ans;
    if (!isEmpty())
        ans = _last->getVal();
    else
        ans = T();
    return ans;
}

/* Return whether the queue is empty or not */
template<class T>
bool LinkedListQueue<T>::isEmpty() { return _first == nullptr; }

/* Return the number of items in queue */
template<class T>
int LinkedListQueue<T>::count() { return _count; }

应用

应用方面，课程中主要重点讲解了Dijkstra的双栈算术表达式求值算法。该算法使用了使用了两个栈，一个存储值，一个存储运算符。它仅对未省略括号的算术表达式有效。且我们为了简化，只考虑二元运算符。它主要要处理下列四种情况：

对于操作数（值），它将其压入到操作数（值）栈中；
对于运算符，它将其压入到运算符栈中；
对于左括号，虽然为运算符，我们将其忽略；
对于右括号，我们从运算符栈中弹出栈顶运算符，并从值栈中，弹出栈顶两个元素（只考虑二元运算符），并根据弹出的运算符，对两个弹出的值进行相应的计算操作。

这里有几个细节需要注意：

因为我们是从左到右扫描，逐个读取处理字符串。所以对于弹出的两个值元素，先弹出的应该是运算符右侧的值（后压入），后弹出的则是运算符左侧的值（先压入）。
课程中是逐个读取字符串，一个字符串代表一个值/运算符。我改为直接输入整行算数表达式。则需要逐个字符处理，对应的，为了判断输入的值是否完整（比如我输入了98,要判断是98而不是9），我们要往前看一位，若接下来一位仍为数字，则将当前结果×10并继续读下一位，若不是，则表明值已经读取完整，将其压入值栈中。

具体代码如下：

/* ArithmeticExpressionUsingStack.cpp */

#include "ArrayStack.h"
#include "ArrayStack.cpp"
#include <string>
#include <iostream>

using namespace std;


/*
 *  Dijkstra's two-stack arithmetic expression evaluation.
 *  One stack for operator, another stack for value.
 *  ・Value: push onto the value stack.
 *  ・Operator: push onto the operator stack.
 *  ・Left parenthesis: ignore.
 *  ・Right parenthesis: pop operator and two values; push the result of applying that operator to those values onto the operand stack.
 *  
 *  WARNING: Arithmetic expressions that ignore parentheses are not considered! And we only care about binary operator (operator with two values).
 */
int evaluate(string input)
{
    ArrayStack<char>* ops = new ArrayStack<char>();
    ArrayStack<int>* vals = new ArrayStack<int>();
    try
    {
        
        int num = 0;
        for(int i = 0; i < input.length(); i++)
        {
            char c = input[i];
            switch (c)
            {
            // Ignore the '(' and ' '[space].
            case '(':
            case ' ':
                break;

            // Pop the operator in 'ops' stack and do the operator.
            case ')':
            {
                char op = ops->pop();
                // if (op == char())
                //     throw "Illegal arithmetic expression!";
                int valR = vals->pop(); 
                if (op == '+') valR = vals->pop() + valR;
                else if (op == '-') valR = vals->pop() - valR;
                else if (op == '*') valR = vals->pop() * valR;
                else if (op == '/')
                {
                    if (valR == 0)
                        throw "The divisor cannot be zero!";
                    valR = ops->pop() / valR;
                }
                vals->push(valR);
                break;
            }

            // Arithmetic operator
            case '+':
            case '-':
            case '*':
            case '/':
                ops->push(c);
                break;

            // Value 
            case '0':
            case '1':
            case '2':
            case '3':
            case '4':
            case '5':
            case '6':
            case '7':
            case '8':
            case '9':
                num = num * 10 + (c - '0');
                // One char of lookahead to deter whether it is a connected number or not. If the value is clear (found the end), push to the 'vals' stack.
                if (i+1 >= input.length() || input[i+1] > '9' || input[i+1] < '0')
                {
                    vals->push(num);
                    num = 0;
                }
                break;
            default:
                throw "Illegal characters in input!";
                break;
            }
        }
        if (vals->count() != 1)
            throw "Illegal arithmetic expression!";
    }
    catch(const char* msg)
    {
        cerr << msg << '\n';
    }
    
    return vals->pop();
}

/*
 *  A simple test:
 *  Input the arithmetic expression(one line) and evaluate it, it will print the answer and wait for next input.
 *  Input 'End' to exit.
 */
int main()
{
    ArrayStack<string>* ops = new ArrayStack<string>();
    ArrayStack<int>* vals = new ArrayStack<int>();

    string input;
    while (true)
    {
        getline(cin, input);
        if (input == "End")
            break;
        cout << "Ans: "<< evaluate(input) << endl;
    }
    return 0;
}

课程作业

这个课程作业要求我们实现两个特殊的队列形式，deque和randomized queue。[具体可以看这](Programming Assignment 2: Queues (princeton.edu))。

Dequeue. A double-ended queue or deque (pronounced “deck”) is a generalization of a stack and a queue that supports adding and removing items from either the front or the back of the data structure.

Dequeue实际上就是可以双头添加/删除的队列，比起queue队头删除队尾添加多了些选择。

Randomized queue. A randomized queue is similar to a stack or queue, except that the item removed is chosen uniformly at random among items in the data structure.

Randomized queue的话，把queue队头删除的特性改为了队列中随机删除。增加了随机性。

代码就不贴了，具体可以看Github仓库里的。

后记

学习参考内容：

Algorithms, Part1 - Coursera

《算法第四版》