构造D-Heap并理解其插入删除算法|学习记录
这几周在痛苦的学习数据结构,老师给我们布置了一个构造D-Heap的作业,断断续续debug了两天,总算是实现了。这里就记录一下我的思路与过程。
什么是D-Heap?
以下为个人目前见解,还在学习中,不一定完全正确。
首先,它是一个堆(heap)结构,我们常说的堆结构Binary-heap(这里以最小堆为例)应该满足以下两点:
- 是一个完全二叉树(这样才能够存储在数组里)
- 每个父节点都要小于其子节点(最大堆相反)
而D-Heap可以理解为其变式,或者称为泛型,它的每个父节点可以拥有D个子节点。
构造D-Heap
Heap是存放在数组中的,通过简单的画格子方法,我们可以找到一个规律(假设我们从下标为0开始存数),第i位的数恰巧为第i * d 到第(i+1) * d位数的父节点,这也是我们构造的关键。
插入
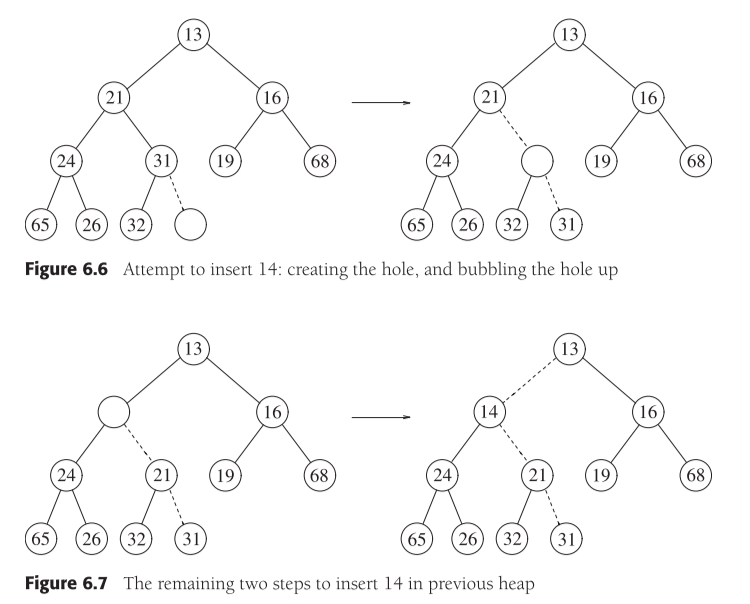
插入的思路如下:
- 将插入的数据存放在队尾;
- 由队尾的叶子开始,与其父节点进行比较,若父大子小,则进行交换,即选较小值作为父节点(默认为最大堆);
- 重复第2步骤,直至不再需要交换或者遍历到了根节点,表明堆已是有序的了。
而由子节点找父节点的方法就用到了我们上面的规律,第(i-1)/d位的节点即使第i位的父节点。
删除
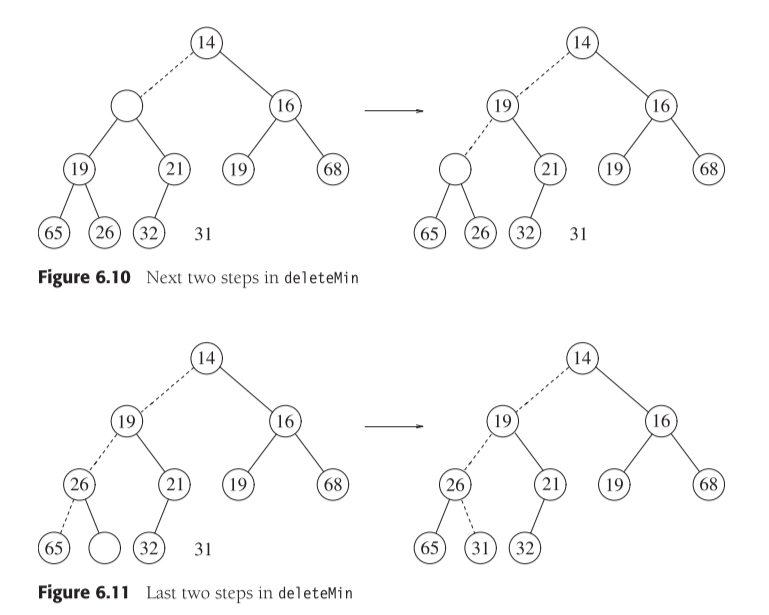
与插入的思路恰好相反,由根节点开始操作:
- 保存好第0位的数据(如果你要返回被删除的值话),将最后一位的数据存放至第0位,覆盖掉,再删除掉最后一位;
- 从根节点开始,找到其子节点(总共有d个)中的最小值,如果父大子小,则交换他们;
- 重复第2步骤,直到交换完最后一层或不再交换。
具体代码实现
这边d我设置为4(按照题目要求),可以修改为一个变量d,在初始化的时候确定。同时为了便于代码的阅读,我将交换(swap)和查找子节点最小数(minInOneSubTree)整合为私有方法。另外又设置了min这个结构,里面存有最小值的大小,对应的下标,以及是否存在(exist,主要用来解决只有1个的极端条件)。代码本身肯定还不够精简,还不是最终版本,可以作为参考。
#include <iostream>
#include <cmath>
using namespace std;
template <class T>
class quadHeap
{
public:
quadHeap()
{
for(int i = 0; i < CAPACITY; i++)
{
data[i] = static_cast<T>(-1);
}
}
~quadHeap()
{
}
void insert(T element)
{
data[currentSize++] = element;
int currentIndex = currentSize - 1;
bool notOrdered = true;
while (notOrdered && currentIndex > 0)
{
notOrdered = swap(currentIndex);
currentIndex = (currentIndex - 1) / 4;
}
}
T deleteMin()
{
T returnElement = data[0];
T lastElement = data[--currentSize];
data[currentSize] = static_cast<T>(-1);
if (data[0] == static_cast<T>(-1))
return returnElement;
data[0] = lastElement;
min minOne;
minOne.data = data[0];
minOne.index = 0;
while (minOne.index < currentSize)
{
minOne = minInOneSubTree(minOne.index);
if (!minOne.exist)
break;
swap(minOne.index);
}
return returnElement;
}
bool isEmpty()
{
if (data[0] == static_cast<T>(-1))
return true;
else
return false;
}
void print()
{
int i = 0;
while (i < currentSize)
{
cout << data[i++] << " ";
}
cout << endl;
}
private:
struct min
{
T data;
int index;
bool exist = true;
};
static const int CAPACITY = 61;
int currentSize = 0;
T data[CAPACITY];
bool swap (int index)
{
if (index <= 0)
{
return false;
}
bool isChanged = false;
int preIndex = (index - 1) / 4;
T temp;
if (data[index] < data[preIndex])
{
isChanged = true;
temp = data[preIndex];
data[preIndex] = data[index];
data[index] = temp;
}
return isChanged;
}
min minInOneSubTree(int index)
{
min minOne;
minOne.data = data[index * 4 + 1];
minOne.index = index * 4 + 1;
if (minOne.data == static_cast<T>(-1))
{
minOne.exist = false;
return minOne;
}
for(int i = index * 4 + 2; i <= (index + 1) * 4; i++)
{
if (data[i] == static_cast<T>(-1))
{
break;
}
if (minOne.data > data[i])
{
minOne.data = data[i];
minOne.index = i;
}
}
return minOne;
}
};
int main()
{
quadHeap<int> testHeap;
testHeap.insert(10);
testHeap.insert(12);
testHeap.insert(1);
testHeap.insert(14);
testHeap.insert(6);
testHeap.insert(5);
testHeap.insert(8);
cout << "Test" << endl;
cout << testHeap.deleteMin() << endl;
cout << testHeap.deleteMin() << endl;
while (!testHeap.isEmpty())
{
cout << testHeap.deleteMin() << endl;
testHeap.print();
}
testHeap.insert(15);
testHeap.insert(3);
testHeap.insert(9);
testHeap.insert(7);
testHeap.insert(4);
testHeap.insert(11);
testHeap.insert(13);
testHeap.insert(2);
testHeap.print();
}
小结
写出来没错就好,也算进步了一点~