Union-Find问题的解决与方案迭代|Algorithms, Part1|第一周
引言
记录一下刷Coursera上《Algorithms, Part1》课程的所学内容。主要包括复现一些课上经典的数据结构与算法(C++),以及每周课程作业的部分(Java)。如有错误之处,欢迎纠正。
正文
课程内容
这周分为两块,一部分为算法课程总的介绍,另一部分则是Union-Find的内容。
课程介绍的部分就不再赘述。我们主要来看看Union-Find的部分。
不过在此之前,我们要知道,算法的目的是为了高效解决问题。我们根据问题情况建立模型,然后找到一种速度尽可能快,消耗内存尽可能少的算法去解决。当然这不可能是一蹴而就的。我们需要不断迭代算法,直到满足需求。接下来的Union-Find就是一个贯彻这一思想的案例。
Union-Find
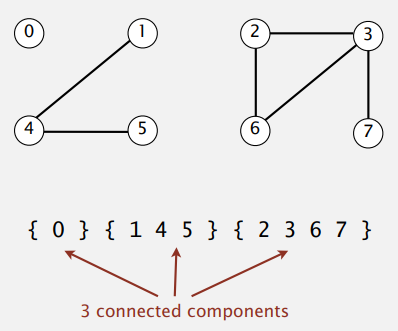
实质就是一个动态连通性的问题,判断两个点之间是否能连通。动态就体现我们可以动态地连接两个点(当然应该也能断开两个点的连接,但是在这里为了简化问题,没有考虑)。于是根据这个问题,我们需要设计一个数据结构来保存程序已知的所有整数对的足够多的信息,并用他们来判断一对新对象是否是相连的。
这个数据结构应该包含以下的几个基本方法:
void unionNode(int node1, int node2):连接两个结点。如果已经连接了,就不再做任何操作。int find(int node):返回该结点的根节点(或者说组号)。int count():返回组数。bool isConnected(int node1, int node2):判断两个点是否连接。
方案一 | Quick-Find
我们使用一个数组来记录它的根结点(或者可以理解为它的组号),只要组号相同,就说明点是连通的。所以我们核心就是维护这个记录根结点的数组。当然为了记录组数,我们还需要维护一个组数的变量。
所以我们对于这几个基本方法的实现思路如下:
void unionNode(int node1, int node2):判断两个结点的根结点是否一致,一致表示已连接,不用再做操作,否则就遍历根结点数组,让node1同组的根节点都变成node2的根节点。同时连接后,组数减一,所以别忘了组数的变量。int find(int node):返回根结点数组的对应值即可。int count():返回表示组数的变量即可。bool isConnected(int node1, int node2):判断两个点是否连接只需要判断他们根结点(组号)是否一致,一致就是连接,反之不是。
除此之外,还加了void Show()这个方法,方便测试调用查看结果。
实现代码如下:
/* Use the quick-find method */
class QuickFindUF
{
private:
int* _root;
int _count;
int length(int* arr) { return _msize(arr) / sizeof(*arr); }
public:
QuickFindUF(int size)
{
_root = new int[size];
// Init, the root is itself.
for (int i = 0; i < size; i++)
_root[i] = i;
_count = size;
}
~QuickFindUF()
{
delete[] _root;
}
/* Check whether these nodes are connected */
bool isConnected(int node1, int node2) { return find(node1) == find(node2); }
/* Union the node1 and node2, let all node's root is same as node1_root to node2_root */
void unionNode(int node1, int node2)
{
int node1_root = _root[node1];
int node2_root = _root[node2];
// Same root, already connect, no need to do anything
if (node1_root == node2_root)
return;
// Connect
int len = length(_root);
for (int i = 0; i < len; i++)
if (_root[i] == node1_root)
_root[i] = node2_root;
_count--;
}
/* Return the identification(root) of the specific node */
int find(int node) { return _root[node]; }
/* Return the number of connected component */
int count() { return _count; }
/* Show the nubmer of nodes, the number of connected component and the "nodes -> it's root" */
void show()
{
int len = length(_root);
cout << "The nodes number: " + to_string(len) << endl;
cout << "The connected components number: " + to_string(count()) << endl;
cout << "Node\t -> it's root" << endl;
for(int i = 0; i < len; i++)
cout << to_string(i) + "\t -> " + to_string(find(i)) << endl;
}
};
这个算法的问题就在于,每次unionNode()时,如果要连接,那就需要遍历整个数组。如果每次都要连接,那么时间开销将会是$O(n^2)$级别的。这是我们不能接受的。
方案二 | Quick-Union
于是我们提出了方案二,这次我们不直接指向根节点,而是指向它的父结点,即从叶子开始,构造了一棵树。而如何判断是根节点呢,只要它的父亲指向它本身即可。
所以我们对于这几个基本方法的实现思路如下:
void unionNode(int node1, int node2):判断两个结点的根结点是否一致,一致表示已连接,不用再做操作,否则就让node1的树作为子树并入到node2的树中,即让node1的根结点的父亲指向node2的根结点。int find(int node):返回根结点数组的对应值即可。int count():返回表示组数的变量即可。bool isConnected(int node1, int node2):与方案一一样,判断两个点是否连接只需要判断他们根节点(组号)是否一致,一致就是连接,反之不是。
另外,在这边我还添加了一个int depth(int node)的函数,返回node结点所对应的深度,方便最后在show函数里显示树最大的深度(这个与我们判断时遍历的最坏情况息息相关)。
实现代码如下:
/* Use the quick-union method */
class QuickUnionUF
{
private:
int* _parent;
int _count;
int length(int* arr) { return _msize(arr) / sizeof(*arr); }
int depth(int node)
{
int dp = 1;
while (_parent[node] != node)
{
node = _parent[node];
dp++;
}
return dp;
}
public:
QuickUnionUF(int size)
{
_parent = new int[size];
// Init, the parent is itself.
for (int i = 0; i < size; i++)
_parent[i] = i;
_count = size;
}
~QuickUnionUF()
{
delete[] _parent;
}
/* Check whether these nodes are connected */
bool isConnected(int node1, int node2) { return find(node1) == find(node2); }
/* Union the node1 and node2, let node1_root's parent to node2_root */
void unionNode(int node1, int node2)
{
int node1_root = find(node1);
int node2_root = find(node2);
// Same root, already connect, no need to do anything
if (node1_root == node2_root)
return;
// Connect, let node1 be the subtree of the node2
_parent[node1_root] = node2_root;
_count--;
}
/* Return the identification(root) of the specific node */
int find(int node)
{
// To find the root, which parent is itself.
while (_parent[node] != node)
node = _parent[node];
return node;
}
/* Return the number of connected component */
int count() { return _count; }
/* Show the nubmer of nodes, the number of connected component, the depth and the "nodes -> it's root" */
void show()
{
int len = length(_parent);
cout << "The nodes number: " + to_string(len) << endl;
cout << "The connected components number: " + to_string(count()) << endl;
int dp = 0;
int tempD;
for(int i = 0; i < len; i++)
{
int tempD = depth(i);
if (tempD > dp)
dp = tempD;
}
cout << "The depth: " + to_string(dp) << endl;
cout << "Node\t -> it's root" << endl;
for(int i = 0; i < len; i++)
cout << to_string(i) + "\t -> " + to_string(find(i)) << endl;
}
};
这样我们每次连接的时候,也只需要执行一步操作了,不需要再整个数组遍历过来。但是我们增加了find()的消耗,同时由于unionNode()里我们也需要使用find()去找根节点。这个方法还是不行。
那么关键在哪?考虑下最坏情况,一颗没有分叉的树,父子都是一对一的,如果从叶子出发,那就需要n次遍历,才能找到根节点。所以我们要想办法缩短这个距离,即让树的高度尽可能的小。
方案三 | Weighted-Quick-Union
在这个方案里,我们在连接树的时候,将树里结点的数量作为权重,越多权重越大,我们让小权重(结点少)的树作为大权重(结点多)的树的子数。从而保证树的高度尽可能的少,减少find()遍历的次数。(关于结点数与树高度的关系,可以从想象从零开始连接独立的结点,构造这棵树出发。)
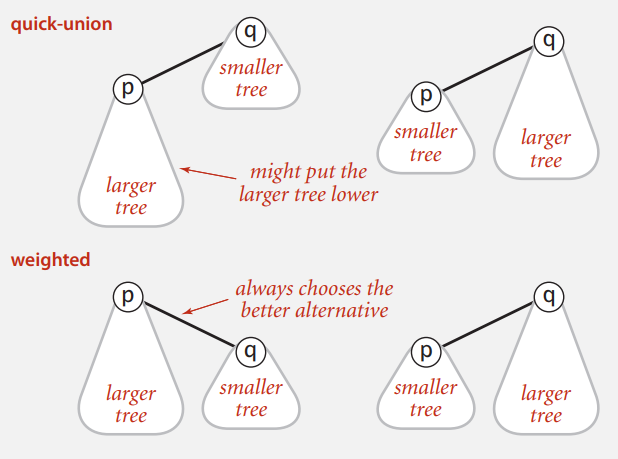
所以我们对于这几个基本方法的实现思路如下:(其他与方案二保持一致的就不再重复)
void unionNode(int node1, int node2):判断两个结点的根结点是否一致,一致表示已连接,不用再做操作,否则就判断两个结点的让node1的树作为子树并入到node2的树中,即让node1的根结点的父亲指向node2的根结点。
实现代码如下:
/*为了减少内容,这边只把与方案二有区别的部分放上来*/
/* Use the weighted-quick-union method */
class WeightedQuickUnionUF
{
private:
int* _size;
public:
WeightedQuickUnionUF(int nrOfNode)
{
_parent = new int[nrOfNode];
_size = new int[nrOfNode];
// Init, the parent is itself ans size is one(only itself).
for (int i = 0; i < nrOfNode; i++)
{
_parent[i] = i;
_size[i] = 1;
}
_count = nrOfNode;
}
/* Union the node1 and node2, let smaller size node root's parent to larger size node root */
void unionNode(int node1, int node2)
{
int node1_root = find(node1);
int node2_root = find(node2);
// Same root, already connect, no need to do anything
if (node1_root == node2_root)
return;
// Connect, let the smaller tree be the subtree of the larger tree
if (_size[node1_root] < _size[node2_root])
{
_parent[node1_root] = node2_root;
_size[node2_root] += _size[node1_root];
}
else
{
_parent[node2_root] = node1_root;
_size[node1_root] += _size[node2_root];
}
_count--;
}
}
这样我们就可以缩减每次find()所需要的时间了,从$O(n)$变为$O(logN)$,但是,有没有可能实现常数级别的查找呢?
方案四 | Path-Compressed-Weighted-Quick-Union
我们可以尝试把路径再一次的压缩,让每次尽可能一次就找到,即让每个结点都直接指向对应树的根结点,同时又不增加过多的额外操作。我们可以在检查结点的同时将它们直接连接到根结点。
所以我们对于这几个基本方法的实现思路如下:(其他与方案三保持一致的就不再重复)
int find(int node):返回根结点数组的对应值,同时将该棵树内的所有结点都指向根节点。(当然我们首先要知道根节点才能指向,所以要用两个独立的循环,一个找根节点,找完后再重新循环一遍,更改根结点。从时间复杂度的角度上分析,只是乘了个两倍的系数,整体不影响。)
实现代码如下:
/*为了减少内容,这边只把与方案二有区别的部分放上来*/
/* Use the path-compressed-weighted-quick-union method */
class WeightedCompressedQuickUnionUF
{
public:
/* Return the identification(root) of the specific node */
int find(int node)
{
int root = node;
// To find the root, which parent is itself.
while (_parent[root] != root)
root = _parent[root];
// Let all its children link directly to the root.
while (_parent[node] != node)
{
_parent[node] = root;
node = _parent[node];
}
return root;
}
}
这样我们就实现了一个简单的路径压缩~这个算法的时间复杂度的均摊开销为$O(1)$,成功实现常数级别的查找与连接了。
这就是我们一步步细化算法的过程了。
课程作业
本周的课程作业内容为Percolation。通俗理解就是判断顶部的水能否一层层过滤渗透到最底下一层。我们使用网格来表示,每个格子都有打开或者关闭两种选项。我们设每个格子被打开的概率为$p$,我们想知道,当$p$恰好为何值时,刚好处于渗透状态。
当然具体内容描述还是得看上方网站介绍。
代码具体内容就是根据他提供的UF类,解决这个具体问题。
关键有两点:
- 为了方便判断顶部到底部是否流通,我们可以构造两个虚拟的点,分别连接顶部一层的结点和底部一层的结点,这样我们只要判断这两个点是否连通即可。
- 当我们将一个结点打开时,要考虑将其与四周(上下左右)方位的已打开结点相连。
代码就不贴了,具体可以看Github仓库里的。
后记
学习参考内容: